Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 캐글
- 심층신경망
- r
- bigquery
- do it
- 쿠버네티스
- ADP 실기
- 리액트
- frontend
- 머신러닝
- python
- 클러스터링
- Machine Learning
- 프론트엔드
- 파이썬
- ADP
- 대감집
- 타입스크립트
- TooBigToInnovate
- 대감집 체험기
- 구글
- Kubernetes
- 최적화
- DBSCAN
- 빅쿼리
- docker
- Kaggle
- 차원 축소
- LDA
- React
Archives
- Today
- Total
No Story, No Ecstasy
[ADP 실기 with R] 4. Correlation, Linear Regression 본문
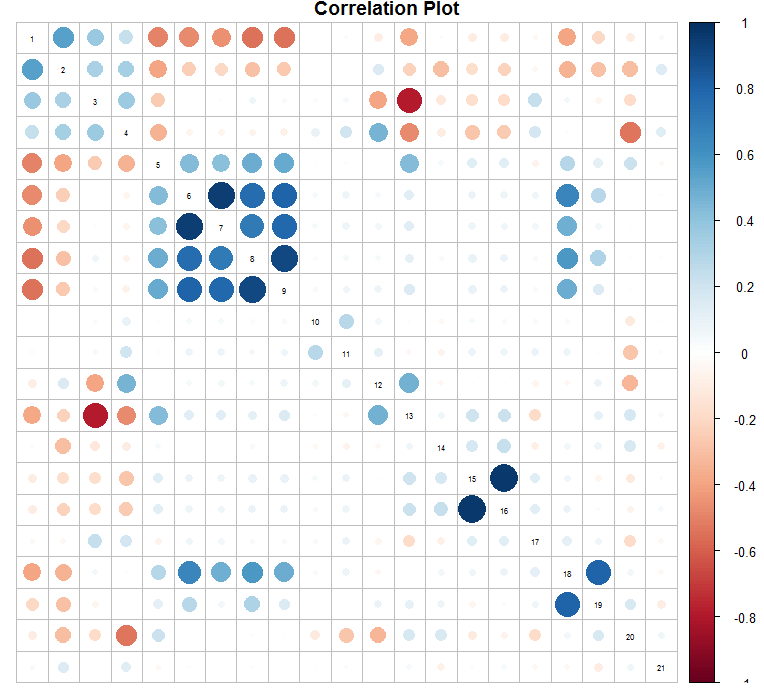
1. Correlation Analysis, 상관 분석
- 두 변수 간 상관관계를 통계적으로 알기 위한 통계분석 방법 (* 인과관계가 아님)
- 상관계수 3종류
(1) Pearson: 두 변수가 모두 정규분포를 따를 시 선형적인 상관관계의 크기를 모수적 방법으로 나타냄
(2) Spearman: 정규분포가 아닌 연속형 변수 or 순서형 변수일 경우, 순위 상관관계의 크기를 비모수적으로 나타냄
(데이터 내 편차와 에러에 민감, 보통 Kendall보다 높음)
(3) Kendall: 변수 간 순위의 일치도가 비슷한 정도를 나타냄 (샘플 사이즈가 적거나, 데이터 동률이 많을 때 유용)
- R 코드 예제
# 1. 상관 계수 결정을 위한 정규성 검정
shapiro.test(data)
# 2. 상관 분석 수행
## - use: everyghin, all.obs, complete.obs, na.or.complete, pairwise.complete.obs
## - method: pearson, spearman, kendall
cor(data, use = "complete.obs", method = "pearson")
# 3. 시각화
## 3.1. 시각화 방법 1
library(corrplot)
corrplot(cor(data, method = "pearson"))
## 3.2. 시각화 방법 2
plot(data)
2. Linear Regression, 선형 회귀 분석
- 독립 변수와 종속 변수 간 선형 인과 관계를 분석하기 위한 기법
- 독립 변수가 여러 개일 경우, 다중공선성이 심각한 것들은 제거해야 한다.
- 허용오차: 0.1 이하면 심각
- VIF (Variance Inflation Factor) = 1/허용오차: 10 이상이면 심각
- 선형회귀분석을 위한 가정을 충족시키는 지 확인해야 한다.
- 선형성, 잔차의 독립성, 잔차의 등분산성, 잔차의 정규성
- R 코드 예제
# 0. package import
library(lmtest)
# 1. step 함수를 활용하여 최적(최소 AIC를 만족하는) 선형 회귀 방정식 결정
## - direction = both, forward, backward 중 선택 (forward, both는 lower부터 시작 / backward는 upper부터 시작)
step.model = step(lm(y ~ x1 + x2 + ... + xn, data)
scope = list(lower =~ 1,
upper =~ x1 + x2 + ... + xn),
direction = "both")
# 2. step.model 바탕으로 선형 회귀모델 생성
## - lm 함수 내부에서 범주형 변수를 dummy 변수로 만든다.
lm.model = lm(y ~ x1 + ... + xk, data)
# 3. 다중공선성 확인
## - 다중공선성이 심각하면 설명력이 더 적은 변수를 모델에서 제거한다.
summary(lm.model) # 허용오차(1 - R^2)을 통해 확인
library(car)
vif(lm.model) # VIF를 통해 확인
# 3. 선형 회귀 모델 가정 충족 여부 검증
dwtest(lm.model) #더빈왓슨 검정을 통한 잔차의 독립성 가정 검증
shapiro.test(resid(lm.model)) #샤피로 테스트를 통한 잔차의 정규성 가정 검증
par(mflow = c(2,2))
plot(lm.model) #plotting을 통한 등분산성, 정규성 검증



