| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 캐글
- 리액트
- Machine Learning
- 타입스크립트
- docker
- 쿠버네티스
- LDA
- 구글
- frontend
- python
- Kaggle
- 파이썬
- 클러스터링
- React
- 빅쿼리
- DBSCAN
- ADP
- TooBigToInnovate
- 머신러닝
- r
- 대감집
- 심층신경망
- Kubernetes
- 프론트엔드
- 최적화
- 차원 축소
- bigquery
- ADP 실기
- do it
- 대감집 체험기
- Today
- Total
No Story, No Ecstasy
HDBSCAN (Hierarchical DBSCAN) 본문
Clustering에는 크게 3개의 방법론들이 있다.
1. Distance-based (ex. K-means)
2. Density-based and grid-based (ex. DBSCAN, HDBSCAN)
3. Probabilistic and generative (ex. Mixture Distributed)
2번 방법론 중 가장 대표적인 예는 DBSCAN (Density based Spatial Clustering of Applications with Noise)인데, HDBSCAN (Hierarchical DBSCAN)은 기존의 계층적 클러스터링 개념을 DBSCAN에 입혀서 기존 DBSCAN이 가진 단점을 보완한 방법론이다.
구체적으로는 DBSCAN의 hyper parameter인 eps를 설정할 필요가 없어지기 때문에, hyper parameter에 대한 튜닝 비용을 상당히 줄일 수 있다.
이 방법론들은 밀도 기반으로 클러스터를 구성하기 때문에, 가까운 데이터가 없는 outliers는 자연스레 클러스터를 배정받지 못하게 되므로, abnormaly or outlier detection을 위해서도 많이 사용된다.
우선 DBSCAN에 대해서 짚고 넘어가면 다음과 같다.
- 각 군집 내 데이터가 최소한의 밀도를 만족시키도록 군집을 구성하는 밀도 기반 기법
- 구형이 아닌 임의의 형태의 군집을 발견하는데 효과적이다.
- noise가 나올 수 있다(클러스터링되지 않는 데이터가 생긴다).

- 알고리즘
1. 무작위로 데이터 선택
2. 선택된 데이터로부터 지정된 거리 안의 모든 데이터(이웃) 탐색
3. 이웃의 개수가 최소기준보다 많으면(아닐 시 noise 처리) 클러스터 생성 후 이웃 확인
4. 이웃이 클러스터에 할당되지 않았으면 해당 클러스터에 할당 후 이웃의 이웃을 탐색
5. 클러스터 내의 모든 이웃에 대하여 더 이상 이웃이 없을 때까지 단계 4를 반복
6. 한 번도 방문한 적 없는 데이터에 대하여 단계 1-4 반복
- DBSCAN은 2개의 hyper parameters(밀도 계산 거리, 거리 내 최소 데이터 개수)를 지정해야 한다.
HDBSCAN은 eps에 따른 DBSCAN 결과를 계층 Tree를 통해 보여주고, 가장 안정적인 클러스터를 보여준다.
- HDBSCAN은 DBSCAN과 계층(Hierarchical)적 군집분석 개념을 통합한 기법
- DBSCAN과 다르게 eps (최소 밀도 거리)를 설정할 필요가 없다. (어차피 결과가 계층구조로 나오기 때문)
- python 코드 예시
import hdbscan
clusterer = hdbscan.HDBSCAN(min_cluster_size=5, gen_min_span_tree=True)
clusterer.fit(data)
HDBSCAN(algorithm='best', alpha=1.0, approx_min_span_tree=True,
gen_min_span_tree=True, leaf_size=40, memory=Memory(cachedir=None),
metric='euclidean', min_cluster_size=5, min_samples=None, p=None)- 알고리즘
1. Density space 생성 (Transform the space)
. core distance of point x for parameter k, core_k(x): 점 x에서 k개의 min_cluster_size를 만족시키는 거리
. mutual reachability distance of point a and b = max{ core_k(a), core_k(b), d(a,b) }
. Noise point에 의해서 서로 멀리 떨어진 클러스터가 하나로 묶이는 것을 방지하고자,
각 점의 sparsity를 반영한 mutual reachability distance를 거리 지표로 사용한다.
. 즉, k의 값이 커질수록 더 많은 점들이 'land'가 아닌 'sea'에 포함된다.
2. Minimum spanning tree of distance weighted graph 생성
. 각 점의 mutual reachability distance를 표현하는 spanning tree를 생성한다.
. 그러나, 모든 점들 간 거리를 계산하는 것은 비용이 너무 크므로, Prim’s algorithm을 통해 최소의 Tree만 구성한다.
* Prim's algorithm: 매순간 총 edge의 길이를 최소화하는 점을 이어가며 모든 점을 잇는 greedy algorithm

3. Build the cluster hierarchy
. Minimal spanning tree를 hierarchy of connected components로 변환한다.
. 일반 hierarchical 클러스터링과 동일한 원리로 진행된다.
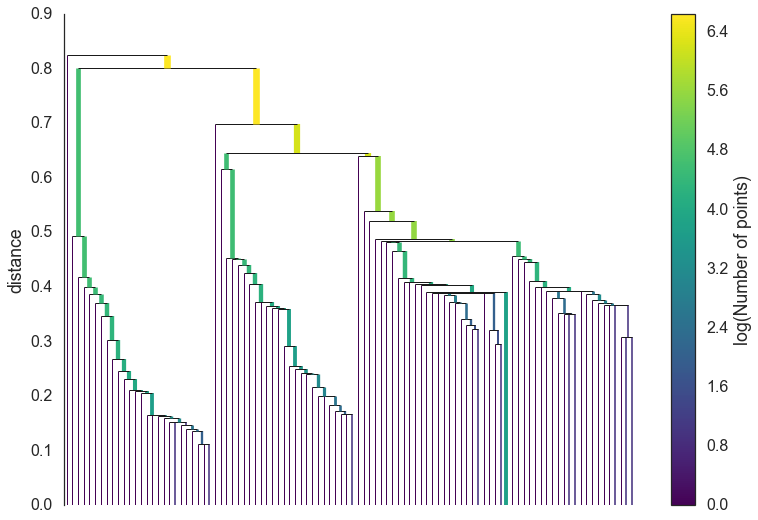
4. Minimum cluster size에 따른 Cluster hierarchy 응축
. min_cluster_size 파라미터를 활용하여 hierarchy의 각 노드를 더 합쳐가며 smaller tree를 만든다.
. 만약 tree의 split points 중 하나라도 min_cluster_size 미만의 점을 가지고 있다면, 합친다.

5. Stable cluster 추출

. 위 식을 활용하여 각 cluster의 persistence를 나타낸다.
. 각 cluster의 stability는 cluster를 구성하는 점들의 람다를 더한 값으로 표현한다.
. 만약 child cluster의 stability가 더 높다면, parent cluster의 stability는 child clusters의 합으로 표현한다.
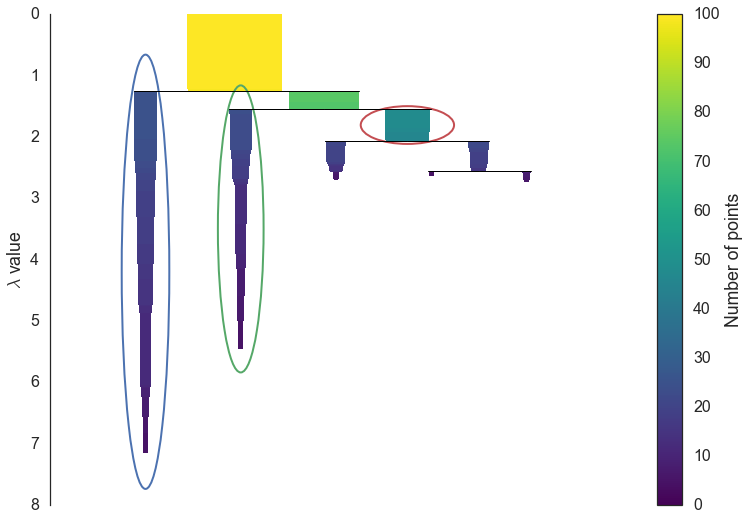

- *** 그러나, HDBSCAN이 항상 DBSCAN보다 좋은 결과를 보장하는 것은 아니다.


HDBSCAN을 DBSCAN과 함께 사용하기 (cluster_selection_epsilon 파라미터)
- 주어진 cluster_selection_epsilon 거리를 활용하여 DBSCAN 수행 후, 나머지 데이터에 대해서 HDBSCAN을 수행한다.
- 이렇게 하면, 원하는 만큼의 밀집도를 가지는 데이터는 하나의 클러스터에 묶이는 것을 보장할 수 있다.
X = np.radians(coordinates)
earth_radius_km = 6371
epsilon = 0.005 / earth_radius #calculate 5 meter epsilon threshold
clusterer = hdbscan.HDBSCAN(min_cluster_size=4, metric='haversine', cluster_selection_epsilon=epsilon, cluster_selection_metod='eom')
clusterer.fit(X)
Hyper Parameter 선택하기
1. min_cluster_size: mutual reachability distance와 condensed tree 구성에 영향을 미치는 가장 직관적인 파라미터
2. min_samples: 높은 값을 줄수록 더 많은 점들이 noise로 분류된다. (최종 클러스터 선정시 constraint로 작용)
3. cluster_selection_epsilon: DBSCAN 알고리즘을 적용할 최대 거리 명시
Reference
https://hdbscan.readthedocs.io/en/latest/
The hdbscan Clustering Library — hdbscan 0.8.1 documentation
© Copyright 2016, Leland McInnes, John Healy, Steve Astels Revision 109797c7.
hdbscan.readthedocs.io
'Data Science Series' 카테고리의 다른 글
| 심층 신경망 (DNN) 훈련 (0) | 2021.05.29 |
|---|---|
| 토픽 모델링 - LDA, Mallet LDA, Guided LDA (0) | 2021.05.27 |
| [Kaggle Visualization] Python basic code (0) | 2021.04.28 |
| [Kaggle Pandas] Python basic code (0) | 2021.04.28 |
| [Kaggle Feature Engineering] Python basic code (0) | 2021.04.28 |


