| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Kubernetes
- 빅쿼리
- Machine Learning
- ADP 실기
- frontend
- 파이썬
- 차원 축소
- 구글
- 심층신경망
- 대감집
- 대감집 체험기
- 쿠버네티스
- LDA
- python
- 리액트
- 프론트엔드
- React
- docker
- 머신러닝
- do it
- 클러스터링
- 캐글
- bigquery
- DBSCAN
- 최적화
- 타입스크립트
- ADP
- Kaggle
- r
- TooBigToInnovate
- Today
- Total
No Story, No Ecstasy
토픽 모델링 - LDA, Mallet LDA, Guided LDA 본문
* 이 글은 rupert님의 블로그의 토픽 모델링 관련 글들을 공부하여 정리한 글입니다.
https://bab2min.tistory.com/567?category=673750
[잠재 디리클레 할당 파헤치기] 1. 베이즈 추론
작년에 토픽 모델링이라는 개념을 접하고 깜짝 놀랐어요. 그냥 적당한 크기의 문헌들을 넣어주면 거기에서 적절하게 컴퓨터가 연관된 단어들을 묶어서 주제 분포를 만들어주고, 문헌별로 주제
bab2min.tistory.com
0. 토픽 모델이란
문서에 등장하는 단어들의 분포를 통해 잠재적인 주제를 발견하는 통계적 알고리즘
1. 베이즈 추론
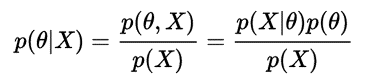
- 토픽 모델링 알고리즘 LDA는 베이즈 추론에 기반한다.
- 베이즈 추론의 순서
1. 어떤 사건이 발생할 확률을 가정
2. 추가적인 관측 발생 시, 그 사건이 발생할 확률을 더 정확하게 추론
- 즉, 관측이 많을수록 더 정확해진다.
- 특정 사건과 짝을 이루는 사전 확률 분포를 켤레 사전 분포라고 한다.
. 이항 분포의 켤레 사전 분포는 Beta
. 다항 분포의 켤레 사전 분포는 Dirichlet
2. 디리클레(Dirichlet) 분포: LDA 의 베이즈 추론에 활용되는 분포
- 베타 분포: 사건 발생 횟수 a-1번, 발생하지 않은 횟수 b-1번 관측 시, 발생 확률 p를 표현하는 분포. B(p; a, b)
- 디리클레 분포: 베타 분포를 k가지 경우를 다루도록 확장한 버전. Dir( p1, ..., pk; a1, ..., ak)
- LDA에서는 베이즈 추론에 이 디리클레 분포를 사용한다.

3. 깁스 샘플링
- LDA는 문서, 단어의 사후 확률을 추정하는 것인데, 단어의 개수가 늘어날수록 계산량이 기하급수적으로 늘어난다.
- 따라서, 이를 빠르고 쉽게 하기 위하여 깁스 샘플링을 활용한다. 깁스 샘플링은 N개의 자료 중 N-1개를 고정하고 한 차원에 대한 자료만 샘플링한 후 합치는 방식으로 진행된다.
- 깁스 샘플링을 활용한 LDA 과정
(1) 각 단어에 임의의 주제 배정,
(2) n번째 단어를 골라서 제외,
(3) 나머지 단어들만으로 문헌의 주제 분포, P(Topic|Document)를 계산하고, 그 단어가 속한 주제의 단어 분포, P(Word|Topic)를 계산한다. 각 분포를 곱하여 가장 높은 확률을 제공하는 Topic을 제외시켰던 n번째 단어에 재배치한다.
(4) 충분히 수렴할 때까지 2, 3단계 반복
- 샘플링 때문에 매번 결과가 달라질 수 밖에 없다. 토픽 개수 K와 hyper parameter 를 잘 튜닝해야 한다.
4. LSA (Latent Semantic Analysis)
- SVD (Singular Value Decomposition): 행렬 데이터의 차원을 축소하기 위해 사용된다.
https://darkpgmr.tistory.com/106
[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
활용도 측면에서 선형대수학의 꽃이라 할 수 있는 특이값 분해(Singular Value Decomposition, SVD)에 대한 내용입니다. 보통은 복소수 공간을 포함하여 정의하는 것이 일반적이지만 이 글에서는 실수(real
darkpgmr.tistory.com
- 문헌-용어 행렬을 특이값 분해를 통해 더 작은 크기의 행렬로 표현하여 잠재적 의미를 분석한다.
(cute animal로 검색해도 kitty나 hamster가 포함된 문헌을 얻어낼 수 있다)
5. pLSA (probabilistic Latent Semantic Analysis)
- 문헌-용어 행렬 내 값을 특정 용어가 등장한 횟수가 아닌, 문헌 내 특정 용어의 등장 확률을 활용한 것
- 확률을 사용하기에 모든 값이 0-1 사이의 값을 가진다. -> SVD를 활용할 수 없게 됨. 대신 NMF를 사용함
- 그러나, 여전히 문헌 내 주제의 분포는 고려하지 않는 것이 약점으로 지적됨 -> LDA가 등장함
6. LDA
- pLSA는 새로운 문헌을 생성해내는 것을 잘 다루지 못했는데, 디리클레 분포를 적용하여 이를 보완함
- 토픽 별 단어의 분포, 문서 별 토픽의 분포를 모두 추정한다.
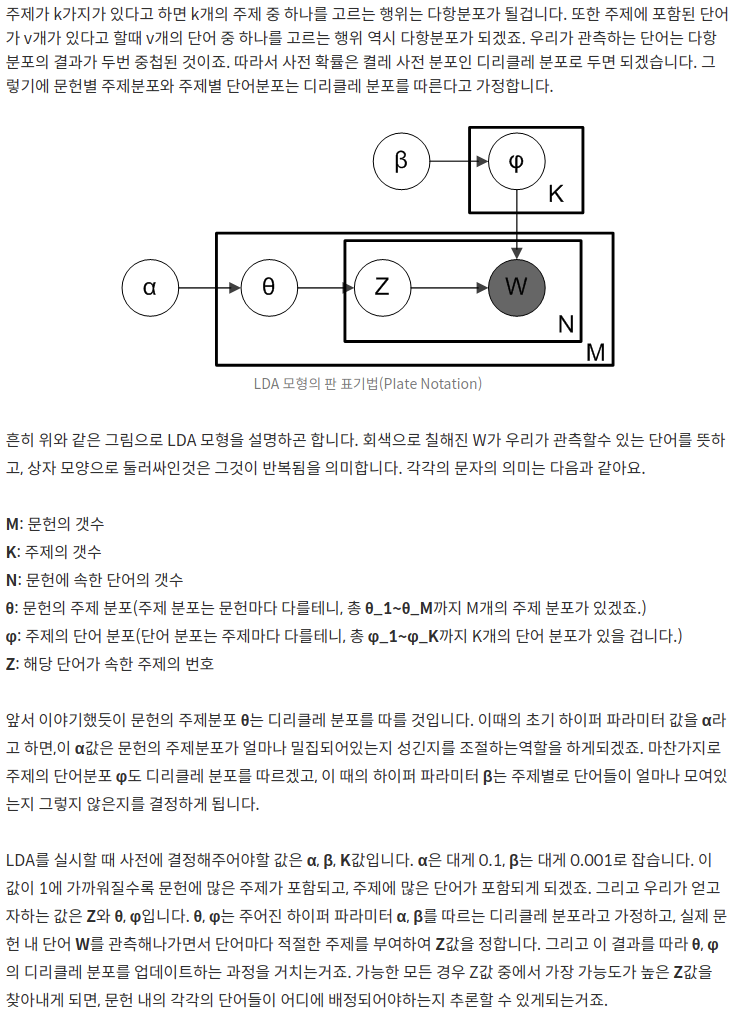
- K개 주제가 있다면, k개 주제 중 하나를 고르는 행위는 다항 분포이다.
- 주제에 포함된 단어 v개가 있다면, v개 단어 중 하나를 고르는 행위도 다항분포이다.
- 이 다항 분포들의 사전 확률을 켤레 사전 분포인 디리클레 분포로 둔다. (즉, 문헌 별 토픽 분포와 주제 별 단어 분포 모두 디리클레 분포를 따른다고 가정한다.)
7. Mallet LDA
- 깁스 샘플링 알고리즘을 최적화(https://mimno.infosci.cornell.edu/papers/fast-topic-model.pdf)
- 시간, 메모리 성능을 높임
8. Guided LDA
- 각 토픽에 seed words를 줌으로써 토픽 분포를 형성하는데 방향성을 제공
- 일반 LDA는 각 단어의 초기 주제가 랜덤으로 할당되는데, 특정 단어들에는 특정 주제의 할당 확률을 높일 수 있음
- LDA의 결과물이 일반적인 인식이나 기대와 너무 다르게 나왔을 경우, 사용할 수 있다.
'Data Science Series' 카테고리의 다른 글
| 오토인코더 (Autoencoder) (0) | 2021.05.30 |
|---|---|
| 심층 신경망 (DNN) 훈련 (0) | 2021.05.29 |
| HDBSCAN (Hierarchical DBSCAN) (0) | 2021.05.25 |
| [Kaggle Visualization] Python basic code (0) | 2021.04.28 |
| [Kaggle Pandas] Python basic code (0) | 2021.04.28 |



